Totalrefleksion i vand
Nedenfor ser vi opstillingen til et forsøg, hvor man søger at bestemme grænsevinklen for totalrefleksion ved overgangen fra vand til luft. En laserstråle sendes ind i et kar med vand, hvori der befinder sig et vippebart spejl. Når spejlet vippes ændres den vinkel, som strålen rammer vandoverfladen med nedefra.

Skærmen bagved tjener til at afsløre, om strålen bryder vandoverfladen, i hvilket tilfælde man vil kunne se en prik på skærmen over vandniveau. I vandet kan strålen ses, idet man i vandet har drysset noget kridtstøv. Nedenfor er et eksempel på en situation, hvor indfaldsvinklen er tilstrækkelig lille til, at der foregår brydning. Man aner dog samtidigt, at en del af strålen reflekteres i vandoverfladen.

Herefter øges indfaldsvinklen indtil strålen ikke kan bryde vandoverfladen, men i stedet reflekteres fuldstændigt (totalrefleksion). Det ses også, at den reflekterede stråle er noget kraftigere end på forrige billede, hvor en del af strålen blev brudt.

Lidt teori
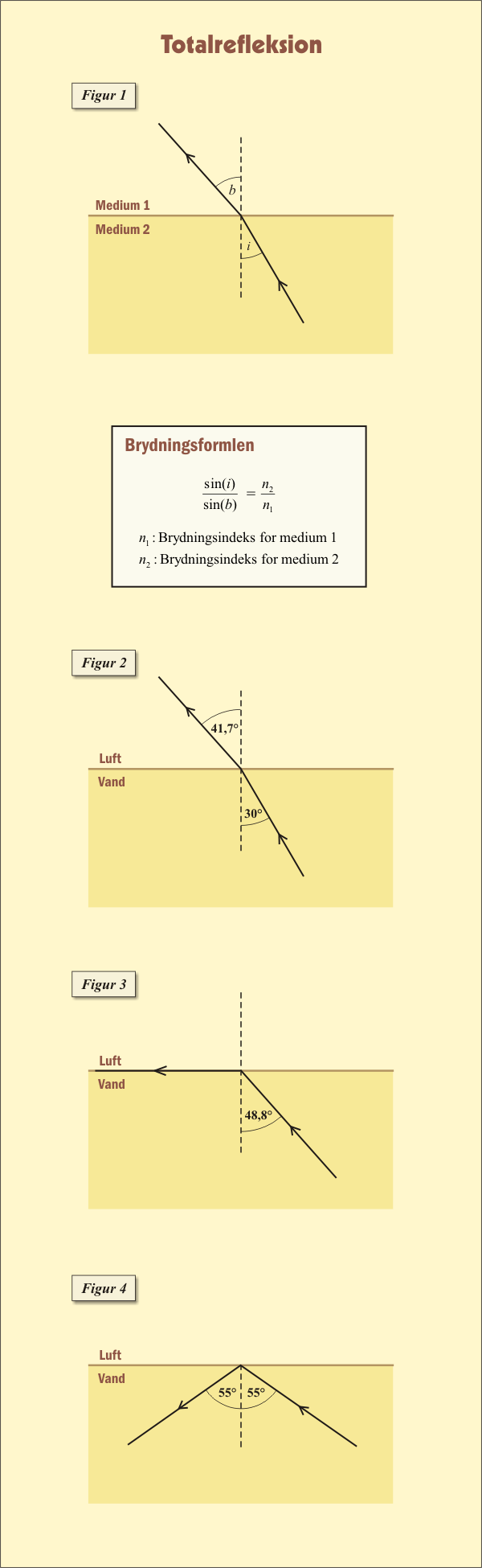
Nedenfor har jeg skitseret princippet for brydning og totalrefleksion. På figur 1 ser vi, at lysstrålen afbøjes ved brydningen, hvilket hænger sammen med, at lyset har forskellige hastigheder i forskellige medier. Dette giver anledning til forskellige såkaldte brydningsindekser for de to medier. Faktisk er brydningsindekset defineret som forholdet mellem lysets hastighed i vakuum og lysets hastighed i det pågældende medium:
![]()
(c står for lysets hastighed i vakuum). På figur 2 ser vi på tilfældet, hvor strålen bevæger sig fra vand til luft. Indfaldsvinklen i er lille nok til, at strålen brydes - eller rettere en del af den. På figur 3 har vi øget indfaldsvinklen til den såkaldte grænsevinkel for totalrefleksion, her 48,75°. Den er karakteriseret ved, at strålen da vil løbe langs med overgangsfladen. På figur 4 er indfaldsvinklen blevet øget yderligere, så hele strålen reflekteres tilbage med samme vinkel, som indfaldsvinklen i.
Princippet i en lysleder
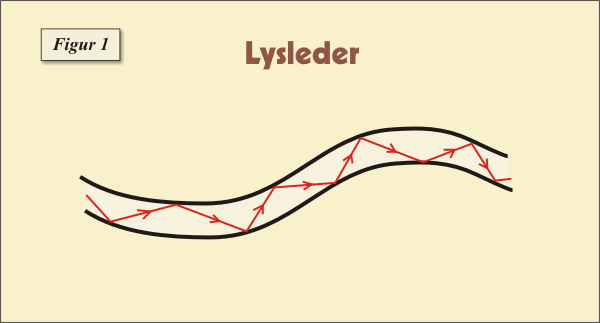
I dette afsnit skal vi illustrere princippet i en lysleder, dvs at lys kan bevæge sig igennem en glastråd uden at slippe ud. Derved kan man transmittere "data" igennem en glastråd. Det viser sig desuden, at der kan transmitteres meget mere information igennem en sådan tråd end igennem en sædvanlig elledning. For at signalet når frem i den anden ende af tråden er det vigtigt, at lyset ikke mister intensitet i væsentlig grad. Det betyder, at man vil tilstræbe, at så lidt som muligt af lyset bryder ud gennem glastråden. Hvis der kun er glastråden og luften udenfor, vil der forekomme totalrefleksion, hvis strålens indfaldsvinkel er større end en vis grænsevinkel (se afsnit om totalrefleksion). Dette vil i høj grad sørge for, at meget af lyset forbliver indenfor glastråden. Af praktiske årsager lægger man dog et ekstra lag glas med et lavere brydningsindeks udenpå den indre glastråd. Dette er illusteret på figur 1 nedenfor.
Forsøg med totalrefleksion i vandstråle
Vi skal ikke foretage et forsøg med en rigtig lysleder. Derimod vil vi vise, at vi kan få det samme til at foregå i en vandstråle. Vandstrålen skabes ved at vand presses ud af en lille tud i bunden af en stor vandbeholder. En Helium-Neon-laser anbringes i tæt kontakt med krukken, så den sender en laserstråle igennem krukken ind igennem tuden og ind i vandstrålen. Opstillingen er illustreret på billedet nedenfor.


På billedet ovenfor ser man, hvordan der er sat en prop med en lille glastud i enden. Der løber en fin stråle vand ud. Det rødlige skær omkring glastuden skyldes i øvrigt, at laserlyset reflekterer lidt i glasset. Det er vigtigt at tilpasse laserstålen, så den rammer midt i dette glasrør. I praksis kan man stoppe vandstålen med en tandstikker. Hvis laserstrålen er rettet rigtigt skal den ene ende af tandstikkeren lyse op, som vist på fotoet nedenfor.

Når man igen tager tandstikkeren ud vil man se, at det røde lys fra Helium-Neon-laseren udbreder sig ned igennem vandstrålen, selv om den buer nedad.

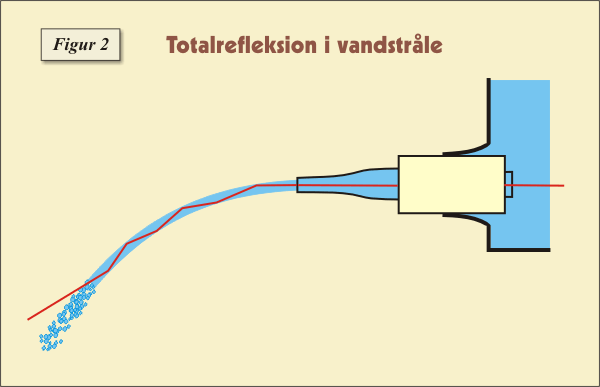
På det første stykke ses næsten intet lys, mens man et stykke nede ser et tydeligt rød lys. Dette fænomen forklares derved, at laserstrålen næsten kun totalreflekterer på det første stykke af vandstrålen (forklarer, at der næsten intet lys ses), mens laserstrålen bryder et stykke længere nede, hvor vandstrålen går fra en fin veldefineret stråle til dråber. Figuren nedenfor viser ideén i forklaringen.
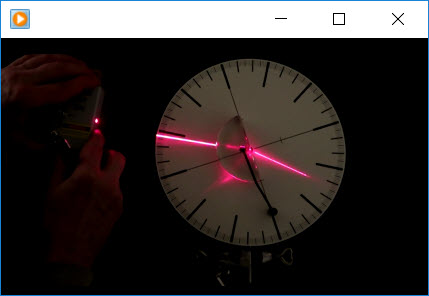
Herunder kan du se et par videoer. Den første handler om, hvordan man med et halvcirkelformet prisme, en gradinddelt skive og en laser kan bestemme grænsevinklen for totalrefleksion for den glassort, prismet består af. I den anden video demonstreres, hvordan man kan sende lys igennem et lyslederkabel.