Mine erfaringer med Maple
Jeg har benyttet Maple siden version 12 og må sige, at jeg er rigtig glad for det. Programmet er ikke perfekt - der er undertiden ting man ville ønske var anderledes. Men det har også været tilfældet for alle de andre CAS-programmer, jeg har set. Maples store force er, at man kan lave et dokument, hvor man glidende skifter mellem skrevet matematik/tekst og beregnet matematik. Det er ikke en nem sag at få sådan noget til at fungere, men Maple er lykkes med det. I andre programmer ender man op med et dokument med et kludetæppe af bokse og særskilte tekst og grafikfelter, som nemt ender med at se meget rodet ud. Et Maple-dokument - derimod - ser generelt rimeligt overskueligt ud og matematikken står knaldflot! Man skal heller ikke undervurdere muligheden for at genberegne en hel sekvens af beregninger i Maple.
Med Knud Nissens såkaldte Gym-pakke (se senere), er det blevet meget bekvemt at løse nogle af de gængse matematikproblemer, der forekommer i gymnasiet, dvs. STX, HTX og HHX. I det hele taget kan enhver, der kan programmere, lave sin egen pakke til Maple, indeholdende speciel funktionalitet.
En anden ting: Maplesoft har de senere år haft heftig fokus på at styrke de interaktive værktøjer i Maple. Det gør det også mere brugervenligt for elever.
Motivation
Et CAS-værktøj er blevet et nødvendigt værktøj i matematik undervisningen. En del opgaver til matematikeksamen kræver adgang til, at der kan foretages komplicerede beregninger eller laves komplekse plots - ting som ville være enten umulige eller tage uhyre lang tid at gennemføre med gamle hjælpemidler såsom en simpel lommeregner og diverse former for papir. På den måde har pensum ændret sig meget de sidste 10 år. Man kan hurtigt nå frem til meningsfulde resualtater og analyser til brug i andre fag såsom samfundsfag, fysik og biologi. Man ser også nogle elever blive mere motiverede af, at de med et CAS værktøj hurtigt kan få noget udført, som de måske ikke var i stand til uden dette hjælpemiddel. I timerne kan man have forløb med eksperimentel matematik, hvor man undersøger ting induktivt og genererer idéer ud fra specieltilfælde. Man ser også elever eksperimentere på egen hånd, og nogle viser det stolt frem, hvis de har fundet nogle smarte måder at løse opgaver på eller få vist noget på - Maples næsten endeløse muligheder kan være en inspirationskilde her!
En fare
Det kan være nærliggende at benytte sit CAS-værktøj til at løse stort set alle typer matematikopgaver. Men der er en fare for, at læringen ender i black boks, hvor eleverne udfører kommandoer eller handlinger bevidstløst uden at vide, hvad der foregår. Derfor bør underviseren tænke meget over tingene i planlægningen. Ofte er det hensigtsmæssigt først at gennemregne sekvenser manuelt for at eleven får en fornemmelse af, hvad der foregår - skridt for skridt. Det er de svageste elever, som hurtigst stiger af her, hvis meningen og hensigten er gemt bag knapper på en computer. Derfor mener jeg, at man også bør styrke det manuelle og prøve at skabe overblik. Hvilke regneregler gælder, og hvilken rolle spiller de med hensyn til at løse opgaver? Stil spørgsmål på tværs i stoffet og undgå hele tiden at falde i fælden med kun at give eleverne "kogebogsopgaver". Der findes værktøjer i dag (og her tænker jeg ikke specielt på Maple), hvor svaret på en opgave fås næsten straks uden at man behøver sætte sig ind i, hvordan maskinen overhovedet er i stand til at give svaret. Her bør man måske stille sig det spørgsmål: Hvis dette værktøj pludseligt ikke længere var til rådighed, ville eleven så være bombet tilbage til start? Det er indsigten, der er væsentlig, ikke resultatet! Man ser det i det på mange måder geniale program GeoGebra, hvis styrke ligger i geometriske konstruktioner og grafiske afbildninger. Men hvad har man lært, hvis man bedes om at bestemme skæringen mellem en parabel og en linje, når man blot kan markere skæringspunkterne og aflæse koordinaterne? Ikke noget matematik, vil jeg sige.
Hvordan starter man med Maple?
Jeg har selv anvendt Maple i diverse matematik og fysikklasser. Min erfaring er, at eleverne (og kollegerne) lige skal over en lille hurdle, før det kører, og man ved, hvordan tingene skal skrives og før man forstår tankegangen bag Maples måde at regne på. Genveje og en liste med typiske begynderfejl kan hjælpe. Det kan også være en god idé at gå langsomt frem på den måde, at eleverne i starten måske bare skal bruge Maple som "skrivemaskine", uden at den skal regne noget ud. I Tekst Mode og i passiv matematik mode kan man skrive flot matematik. Dernæst kan man gå roligt frem ved kun at introducere få nye kommandoer af gangen, fx plot og solve. Skærmvideoer og instruktionsdokumenter kan også være en hjælp. Lad eleverne arbejde en del selv - der er nemlig stor forskel på, hvor hurtigt eleverne arbejder sig fremad. Efter lidt tid er det vigtigt, at man forklarer, hvordan Maple udfører kommandoer - at man kan markere et område og få kommandoerne i dette område genberegnet.
Maple kan regne med enheder!
Som nævnt har jeg også benyttet Maple i fysik. Især det at programmet kan håndtere enheder og præfikser og omregne mellem dem er værdsat blandt eleverne. Her et eksempel på beregning af massen af 0.563 mL sprit:
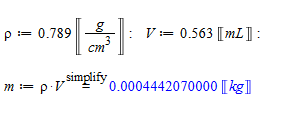
Jeg ser undertiden folk, som ikke regner med enheder, når de bruger Maple i fysik. Der regnes blot med tal, hvor enhederne er underforstået. Det er efter min mening en dårlig idé. Herved går man glip af mere end halvdelen af Maples fordel. Kun i særlige tilfælde, herunder ved regression og tegning af grafer, undlader jeg enheder. Maple kan sagtens løse ligninger, hvori der indgår enheder!
Pædagogisk?
Det er klart, at læreren skal overveje, hvordan han/hun bedst benytter Maple pædagogisk i undervisningen. Jeg ved der er lærere, som synes det var bedst helt uden CAS-værktøj og andet elektronisk udstyr, og at man lærer matematik bedst i hånden. Jeg ved også, at der er lærere, som synes vi skal benytte elektroniske redskaber så meget vi overhovedet kan komme afsted med det. Jeg har personligt et ben i hver lejr. Jeg begræder, at eleverne gør så lidt ud af brøkregning, forholdsregning og lignende i folkeskolen. Da der var et vindue åbent for denne form for indlæring i en tidlig alder, blev chancen forpasset. Meget tyder på, at det bliver væsentligt sværere at tilegne sig disse kompetancer i en senere alder. Jeg mener dette får konsekvenser i algebra siden hen, og det gør det sværere for eleverne at læse en matematisk tekst, hvis de ikke forstår symbolikken og kan håndtere det i hovedet og tænke træk fremad ... Igennem alle tider har man skippet nogle gamle metoder, når ny teknik blev udviklet. I 1500-tallet regnede man på regnebrætter. I 1600-tallet kom logaritmetabeller til og overtog noget af det omstændelige regnearbejde, indtil lommeregnere kom til i 1970'erne. Der var ingen grund til mere at kunne regne med tabeller. Men det er farligt at sige, at man ikke længere behøver kunne regne med en brøk, fordi en maskine kan klare det for én, for så fjerner man selve forståelsen af begreberne. Det vil være rimeligt at skære en smule ned og så bruge den sparede tid til at se på, hvordan man kan komme videre med maskinerne. På samme måde med CAS-regnere: Man bør stadig kunne udregne simple eller mellemsvære differentialkvotienter for forståelsens skyld, men derudover bliver et Maple et glimrende redskab til at komme videre ... undersøge ting om funktioner, som ville være umuligt eller for omfangsrigt at gøre uden. Der er altså en helt ny verden, som åbner sig for os. En verden, hvor vi kan eksperimentere løs!
For forståelsens skyld regner jeg stadig med matematik og fysik "manuelt" på tavlen, når ting bliver gennemgået, og eleverne får også nogle opgaver at regne manuelt. Det samme er tilfældet med fysiske enheder. I øvrigt giver forståelse for enheden også en forståelse for den bagvedliggende fysik. Når det er sagt, så hører jeg ikke blandt dem, der insisterer på, at eleverne selv skal regne med enheder manuelt, når de løser afleveringsopgaver i fysik. Eleverne ville muligvis blive en smule bedre til at regne med enheder manulelt, men det står ikke mål med anstrengelserne. Kompetencerne i brøkregning fra folkeskolen er simpelthen for svage! I evalueringsrapporterne fra studentereksamenerne i fysik A nævnes det da også ofte, at der laves mange fejl i enheder. Man opfrodres ligefrem til at få et CAS-værktøj til at regne dem ud ... Selv om eleverne havde været skrappe til den grundlæggende matematik villle jeg nok alligevel have brugt et CAS-værktøj, for det frigiver tid til andre aspekter i fysikundervisningen. Faktisk kan man hævde, at Maple på et punkt bidrager til en styrkelse af enheder i fysikundervisningen: Eleverne er nødt til at kende enheden for en given fysisk størrelse for at kunne regne med enheder hele vejen. Tidligere så man en del elever kun skrive enheder på slutresultatet og ikke på de mellemliggende udregninger ...
Men der er som lærer i høj grad noget at tænke over selv og diskutere med kolleger: Hvad skal vi undervise i, hvordan skal vi gøre det, hvad er målet og hvordan sikrer vi os, at eleverne opnåret brugbart kendskab til matematik?
MapleCloud
Den store nyhed i version 14 af Maple var MapleCloud. Ideén i MapleCloud er, at man kan anbringe sine Maple dokumenter på en sky, hvorved det er meget nemmere at distribuere sine dokumenter. Denne facilitet har jeg udnyttet med fordel i timerne. Tidligere skulle elever tage deres egen computer med op til tavlen for at tilslutte den projektoren eller tage en USB pen indeholdende filen med, hvorefter filen skulle åbnes på min computer. Bagefter skulle man finde frem til den del af en eventuel lang besvarelse, som vi skulle kigge på i fællesskab på klassen. Nu beder jeg blot en elev markere den del af en besvarelse, som vi vil kigge på og udelukkende lægge denne del af besvarelsen op på skyen. Få sekunder senere kan jeg se elevens opgavebesvarelse i Maple Cloud panelet på min egen computer og vise indholdet på projektoren for hele klassen til diskussion. Samtidig kan de øvrige elever også se elevens bidrag i deres paneler i Maple. Jeg har nemlig på forhånd oprettet en såkaldt gruppe, hvori eleverne er blevet optaget. Det gøres én gang for alle. Det siger sig selv, at for at alt dette fungerer skal eleverne og læreren være online. I praksis er det Maple, som har stillet nogle servere til rådighed. Opgavediskussioner er altså blevet meget nemmere, og man kan bruge tiden på at diskutere egentlig matematik/fysik i stedet for at bruge lang tid på at lade en elev skrive en opgavebesvarelse op på tavlen. Man kan endda regulere størrelsen af tekst/formler via en knap i Maple.
Hvordan bør man bruge Maple?
Når man får et nyt redskab som Maple, opstår hurtigt spørgsmålet om, hvordan man skal besvare opgaver med de nye muligheder. Hvor meget skal man skrive? hvor meget skal man dokumentere? Min egen holdning her er: Ligesom dengang man skrev i hånden, skal man skrive passende kommentarer med tekst og skreven matematik undervejs, så tankegangen i opgaveløsningen klart fremgår. Med Maple får man desuden udvidede muligheder for at dokumentere med grafer - fx ved regressioner, og de bør ofte udnyttes. Alle opgaver/delopgaver skal afsluttes med en konkluderende linje med tekst og resultater. Det skal stå klart hvad resultatet af opgaven eller delspørgsmålet er. I fysik skal resultater skrives passende afrundet - undervejs frarådes det, da kan man blot bruge de sædvanlige 10 cifre, som er default. Desuden skal resultatet angives med enheder. Når alt dette er sagt, bør det også understreges, at man ikke pludselig skal til at komme med yderligere dokumentation, blot fordi man bruger et CAS-værktøj. Det gælder om at få et godt flow i opgaveløsningerne. Nogle elever skriver opgaveformuleringen af i starten af dokumentet. Det bør undgås, simpelthen fordi det tager tid uden at give points. I flere eksamensevalueringer fra ministeriet fraråder man det da også.
Sections kan bruges på en konstruktiv måde til at skrive overblik, også for læreren, der skal rette opgaver. Bed derfor eleverne om at lave en section for hver opgave samt underafsnit til delopgaverne a, b, c, ... Man kan indsætte sidetal m.m. via menuen View > Header Footer... Det kan være fornuftigt for eleverne at lave en skabelon til et dokument, så eleverne ikke skal oprette disse hver gang.

Et godt råd er: Keep it simple! Når jeg løser ligninger, gør jeg det normalt uden restriktioner og sorterer blot eventuelle løsninger udenfor definitionsintervallet eller komplekse løsninger fra i hovedet og angiver kun de relevante på en konkluderende linje. Det sparer en masse tid med at finde ud af, hvilken syntaks der skal til for at fjerne løsninger. Og det er faktisk ikke så nemt at fjerne de komplekse løsninger på en god måde ...
Er der brug for flere programmer - kan Maple det hele?
Det er nok så meget sagt, men Maple er altså et af de to største CAS-værktøjer i verden, så det kan rigtig meget. Jeg prøver selv at undgå at bruge for mange forskellige programmer, da det trods alt tager tid at sætte sig ind i nyt, både for mig selv og for eleverne. Det kan nemt blive for flagrende, hvis man springer fra det ene program til det andet. Jeg bruger Maple langt det meste af tiden. Selv om Maple også kan lave animationer, så bruger jeg dog undertiden det gratis program GeoGebra her. Det er nemt at gå til, og det er genialt til både geometriske konstruktioner og animationer. I fysik bruger jeg Logger Pro til dataopsamling og databehandling, men Maple til fysikopgaver.

